Medical Imaging
Learning Objectives
- Explain what medical physics is and how it has arisen
- Understand all of the basic imaging modalities in medical imaging ranging from X-Rays, CT, PET, Microscopy & OCT
The Beginnings of Medical Physics
With every advancement in science and technology, there have been curious minds trying to apply the knowledge learnt to the human body; attempting to understand the hidden secrets of nature. Medical physics is exactly that applying physics and engineering to the human anatomy.
The following is a brief timeline of these significant milestones, that have helped shape medical physics that we know and love today:
BC Before Christ
| Year | Innovator | Milestone |
|---|---|---|
| 1600 | Egyptians | The treatment of abscesses using a fire drill, is described in the Edwin Smith Surgical Papyrus. |
| 480 | Hippocrates | Wrote about the use of thermography. In his day, mud was spread over the patient’s affected areas. The parts that dried first were thought to indicate underlying organ pathology. |
AD Anno Domini
| Year | Innovator | Milestone |
|---|---|---|
| 965 | Alhazen (Ibn al-Haytham) | Specialised on optics, especially the physics of vision and helped to greatly move the scientific movement forward at the time. |
| 1508 | Leonardo da Vinci | Discovered the principle of the contact lens. One of the world’s first medical physicists, he was fascinated by biomechanics. |
| 1611 | Santorio Santorius | Created the first clinical thermometer. |
| 1673 | Antonie van Leeuwenhoek | Invented the microscope. |
| 1680 | Giovanni Borelli | Related animals to machines and used mathematics to prove his theories. He is regarded as one of the founding fathers of biomechanics. |
| 1780 | Luigi Galvani | Showed that a frog’s legs twitch when placed in a circuit with 2 dissimilar tools. He realised that this was a form of ‘animal electricity’ from the muscle. |
| 1799 | Alessandro Volta | Invented the battery and founded the basis of electrochemistry. He discovered this by taking Luigi’s work one step forward by demonstrating that a brine-soaked cloth could be used instead of a frog’s legs. |
| 1836 | René Laennac | Created the stethoscope. |
| 1835 | Michael Faraday | Contributed significantly to the field of electromagnetism and started to lecture physics at St George’s university. |
| 1850 | Hermann von Helmholtz | Inventor of the ophthalmoscope, to inspect the retina and other parts of the eye. |
| 1890 | Professor Reinold | In this decade physics became compulsory in UK undergraduate medicine. Academic physics departments were established in medical schools across the country with, Prof. Reinold being the first lecturer of Physics at Guy’s Hospital. |
| 1895 | Wilhelm Roentgen | Discovery of x-rays and circulates famous image of wife’s hand. |
| 1896 | Henri Becquerel | Discovered radioactivity but also experiences an adverse effect two years later where he receive’s a burn from a piece of radium in his pocket, taking several months to heal. |
| 1896 | Thomas Edison | Reports eye injuries from x-rays with further symptom reports from others later on in the year including hair loss, reddened skin, skin sloughing off, and lesions. |
| 1898 | Wilhelm Roentgen | Committee of the Roentgen Society on x-ray dosage is established due to the adverse effects and injuries caused by x-rays. |
| 1901 | Henri-Alexandre Danlos | Treats lupus using radium brachytherapy, which involves implanting radioactive materials directly into the affected tissue |
| 1903 | George H. Stover | First radium treatment of skin cancer, he experimented on himself but sadly died early due to excessive radiation exposure. |
| 1904 | Clarence Dally | First person to have reportedly died as a result of x-ray exposure. |
| 1910 | - | Treatment of ringworm arises, extending its applications to the treatment of acne, skin cancers and fungal infections. |
| 1913 | - | Baltimore introduces radium teletherapy, now the most common form of radiotherapy where ionising radiation is pointed at the affected area of interest. |
| 1919 | Sidney Russ | Builds a teletherapy machine at Middlesex Hospital using 2.5g radium left over from the great war. It has deeper penetration than x-rays and a better depth dose than radium packs. |
| 1923 | Dr Alfred Henry Fuson | Killed after falling from a roof during radio experiments. |
| 1930 | - | First megavoltage x-ray system at MGH and Barts . |
| 1934 | Paterson & Parker | ‘Manchester System’. |
| 1942 | - | Cyclotron-produced iodine-131 is used for treatment of hyperthyroidism, four years later it is also introduced as a treatment for thyroid cancer. |
| 1946 | Mayneord & Mitchell | Cobalt-60 therapy |
| 1949 | Harold Johns | Betatron is invented, a device which accelerates electrons in a circular path by magnetic induction. |
| 1950 | - | Medical Ultrasound |
| 1951 | William Mayneord | Rectilinear scanner, an imaging device to capture emission from readiopharmaceuticals in nuclear medicine. |
| 1953 | - | First linear accelerator is established in Hammersmith. |
| 1960 | Anger | Gamma camera. |
| 1964 | - | Technetium-99m is established as the tracer of choice. |
| 1973 | Hounsfield | Computed Tomography (CT). |
| 1973 | Lauterbaur & Mansfield | Magnetic Resonance Imaging (MRI). |
| 1975 | - | Positron Emission Tomography (PET) is created. |
| 2000 | - | Multimodality Imaging. |
Note: You don’t have to learn this - its just for fun!
An interesting point to note is that physicists are not involved in clinical use, because as soon as a medical instrument/device is applied it becomes a doctors field and expertise. But this groundbreaking equipment that medical physicists have created have shaped the future of medicine, greatly increasing the accuracy and reliability of patient’s diagnosis/prognosis.
The Scope of Medical Physics
With the quick progression of medical physics a lot of new areas have arisen, and now medical physicists have a large range of responsibilities ranging from a more physics based to a more engineering based:
| Increased physics content |
| Radiotherapy physics |
| Radiation protection |
| Diagnostic radiology |
| Nuclear medicine |
| Magnetic resonance imaging |
| Ultrasound |
| Non-ionising radiation |
| Physiological measurement |
| Biomechanics |
| Medical electronics |
| Assistive technology |
| Medical engineering design |
| Medical equipment management |
| Increased engineering content |
Today we are going to focus on the Medical Imaging side of the course, which uses of the properties of tissues in the human body to create 2D/3D images depending on the imaging modalities. Here is a video of the course director, Prof Kawal Rhode, introducing all the basic imaging modalities found in an hospital:
Video
Kawal introduces the module to the students and briefly walks around the hospitals showing what each scanner looks like in real life - get all the students excited!
X-RAYS
Video
Introduction
X-Ray imaging involves forming X-Rays using an X-Ray tube:
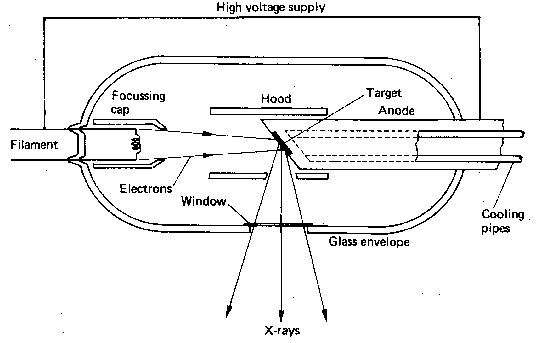
$ Diagram showing a basic X-Ray tube $
This is made up of a a cathode filament surrounded by floating caps. The cathode targets electrons at the target anode. Causes X-Rays to be fired off. Due to the Bremsstrahlung effect, Electrons are deflected and decelerated by the nucleus and, thus, lose energy. In the form of an X-Ray photon, which is fired off. A glass envelope with a small window surrounds this set up, to make sure X-Rays are sent to the target area only. This is further surrounded by a lead shield also with a small window. To avoid excessive exposure to X-Rays.
Attenuation
X-Rays are attenuated by the tissue due to the photoelectric effect and Compton scattering Attenuation dependent on density of tissue and type of tissue material. Each tissue has a specific attenuation coefficient (μ). The remaining intensity of X-Ray photons is detected by the detecting array (again as a result of the Photoelectric effect and Compton scattering) A negative image is formed (highest intensity corresponds to greatest attenuation) Great for imaging bone structures as bones attenuate X-Rays far more than surrounding soft tissue, giving sharp contrasts.
Passageways in the body (i.e. the Gastrointestinal tract and the Blood vessel systems) can be imaged too, by using contrast agents:
- Barium
- Iodine
- Barium and air
Computed Tomography CT
Video
Show how interpolation works using an animation
Introduction
CT scans use X-Rays but instead of a 2D image, a 3D image/representation is created using multiple planar cross section from the body.
We use this instead of planar X-Rays because:
- There is poor soft tissue contrast in planar X-Rays, so imaging areas of soft tissues (such as the brain) is really difficult.
- There is no sensitivity to depth; it is difficult to tell whether a feature imaged is closer to the camera or farther away compared to another feature.
- This is because the camera only picks up the levels of attenuation of the tissues that the X-Rays have passed through, so it has no way of measuring depth.
- What if we take multiple 2D images from different angles?
CT scan involves the following set up:

Diagram showing a basic CT-Scanner set-up array, from the transverse plane.
The detector array and the X-Ray source rotate along the rotating array to take one slice of the patient.
The fan shaped beam, rotation-only mechanism and multiple detectors allow for a much faster image-capturing process and to reduce the dose given of the harmful ionising X-rays.
Due to the nature shape of the beam and the fact that the majority of the attenuation occurs in the middle of the fan beam, a bow tie filter is used.
This allows for the X-Ray intensities at the edges of the beam to be reduced while the middle intensities stay high resulting in a roughly uniform intensity of X-Rays at the detectors.
Detectors are often made from a solid-state device which uses scintillation, photon capture and light-photo-diode signal.
Note: Previous detectors used pressurised xenon gas and this was ionised by the X-Rays to detect the level of attenuation.
CT Number
The tissues ability to attenuate the X-Rays is known as the attenuation coefficient but in CT, this is “normalised” to the CT number (measured in Hounsfield units):
$ CT = \frac{\mu_{tissue} - \mu_{water}}{\mu_{water}} \times 1000 $
Hounsfield units are the standard units for CT number in medical imaging with water at 1000 HU and air at -1000 HU.
Filtered Back projection
An object is resolved using the filtered back projection:
- Multiple images are taken at several angles.
- Each result is then projected back (like a smear) across the reconstructed image.
- The resulting image is a result of putting together all the smeared images
- The area of highest intensity would be the position of the object that had the highest attenuation.
 > Diagram showing how the 1 dimensional intensity map is “smeared” across 2 dimension, and then added with the smears from different directions.
> Diagram showing how the 1 dimensional intensity map is “smeared” across 2 dimension, and then added with the smears from different directions.
To reduce blurring, a sharpening filter mask may be used resulting in the following:

Example of a basic circle having gone through filtered back projection.
CT techniques
To save more time and further reduce the dose given to the patient, one can rely on interpolation techniques and, therefore, make helical scans.
The principle behind this is for the table to move across the rotating array, while the X-Ray source and detectors rotate, resulting in a helical acquisition pattern, rather than lots of parallel circular slices:

Diagram showing a comparison of circular vs helical scans.
Data is reconstructed through information gathered from 180 degrees each side of the reconstruction position.
The speed of the scan is based on the helical pitch:
$ Helical \ Pitch = \frac{Distance \ travelled \ by \ the \ table \ for \ each \ rotation}{Width \ of \ the X-Ray \ beam} $
Image acquisition
The resulting 3D image would be interpolated using interpolation techniques Interpolation is the process by which the data for a point is approximated through mathematically mapping this point using the data points surrounding.
An average interpolator would find the average between the two data points directly before and after it’s position in the dataset.
A quadratic interpolator would try to establish a quadratic relationship between the interpolated data points and the data points surrounding it.
{could insert brief interpolation video here or refer to the medical imaging section }
Magnetic Resonance Imaging MRI
Introduction
So why use MRI instead of the other methods?
- While X-Rays scans and CT scan use ionising radiation (X-Rays), MRI uses completely non-ionising radiation.
- Like CT scans, there is excellent tissue contrast.
- It also has a very high resolution and is, therefore, really very versatile.
- It has a large field of view and imaging can be acquired in any plane (in contrast, CT scans are only acquired in the transverse/axial plane then has to be reconstructed to the other planes)
- MRI has a large field of view
Why not just use MRI?
- MRI is extremely time-consuming
- It is uncomfortable for patients in the MRI due to the loud noises and there being really little space inside the bore (could be claustrophobic inside the MRI machine)
- There are potential harms if the safety regulations are not fully followed
- It is very expensive
- Image acquisition and processing is very complex and there could be imaging artefacts from motion and metal
- Very prone to motion artefacts as the image acquisition process is very time consuming.
Background - Nuclear spin
There are two sources of magnetic fields: - one is moving charges - another is the intrinsic spin property of fundamental particles.
The concept of magnetisation for MRI begins with the idea that there is an intrinsic spin within a nucleus, or, more importantly, the spin of all fundamental particles.
Fundamental particles all have an intrinsic property of spin resulting in the spin angular momentum of the particles.
This is a quantum mechanical property of the fundamental particles and results in a Magnetic moment in these particles.
This is a non-classical property and can be understood further through quantum mechanics Effectively, the particles can be modelled as a bar magnet or even a compass needle (in the diagram below, the curved arrow represents the direction of spin, while the big red arrow represents the direction of the magnetic moment vector)

Diagram showing a simple spherical model of a nucleus (left) and comparing it to a bar magnet (right).
Note: The Stern-Gerlach experiment came up with experimental evidence on the idea of quantum model of spin up and spin down on atom in an area of non-uniform magnetic field. Firing silver atoms through a non-uniform magnetic field resulted in the spins being in two discrete orientations (spin up and spin down as predicted by Quantum) rather than random orientations (as predicted by the classical models).
A compass needle aligns with the earth’s magnetic field. Similarly, the magnetic moment of the nucleus aligns with an external magnetic field.

Diagram showing a comparison of nuclei in a vacuum with no magnetic field (left) and an external magnetic field (right).
However, if the nuclei shown above were static (i.e. not spinning, but still possessed the magnetic moment) then the above diagram would be realistic.
In reality, the nuclear spins do not align directly with the external magnetic field.
In simple terms, the spinning nucleus has an angular momentum and an external magnetic field will apply a force, generating a torque on the angular momentum of the nuclear spin.
The angular momentum will “resist” this torque and, therefore, will not fully align with the external field; instead, it will have a precession around the field lines.
Therefore, the spin magnetic moments of the nuclei never fully align with the magnetic field lines but will go along a precession around the field lines
This can be visualised like a spinning top when it doesn’t spin completely vertically. Imagine a wobble on the spinning top, due to the gravity of the earth. Similarly, the nucleus “wobbles” around the magnetic field lines.
The precession has a frequency (ω0) that can be calculated based on the external magnetic field (B0) and the gyro magnetic ratio (γ) of the nucleus. This ratio changes for different particles and for different compounds (H2O will have a different gyromagnetic ratio on the Hydrogen proton compared to H2)
The frequency will depend on factors such as the initial angular momentum of the nucleus, the type of nucleus it is etc. The spins will either be parallel (up) to the magnetic field or anti-parallel (down) to the magnetic field. Now these are the two energy states of the nuclei as they are made up of protons and neutrons. The quantum nature of subatomic particles mean that there cannot be intermediate energy levels; only discrete quanta such as spin up and spin down.
Generally, more will be parallel, since this is a lower energy state:

Diagram showing nuclear precessions around field lines.
Governed by this equation (where N↑ is the number of parallel spins and N↑ is the number of anti-parallel spins):
The spin of the nucleus is really the spin of the nucleons (proton or neutron). They both have cancelling spins. Therefore, for a nucleus to have a non-zero spin, it will need an unbalanced nucleus. This results in “non-zero spin”:
Nuclei with non-zero spin
The following are a group of nuclei with non-zero nuclear spin:
| Nucleus | Spin | Relative Sensitivity | Natural abundance (%) |
|---|---|---|---|
| 1H | 1/2 | 1.00 | 99.98 |
| 13C | 1/2 | 1.59 x10-2 | 1.11 |
| 14N | 1 | 1.01 x10-3 | 99.63 |
| 15N | 1/2 | 1.04 x10-3 | 0.37 |
| 17O | 5/2 | 2.91 x10-2 | 0.04 |
| 19F | 1/2 | 8.30 x10-1 | 100 |
| 23Na | 3/2 | 9.25 x10-2 | 100 |
| 31P | 1/2 | 6.63 x10-2 | 100 |
It can be seen a normal hydrogen atom has the greatest sensitivity to external magnetic fields. In addition, the concentration and abundance of Hydrogen is highest in the body compared to the other nuclei.
If all the magnetisation vectors of the Hydrogen nuclei are then added up, the directions of the vectors are such that the horizontal components (perpendicular/transverse to the magnetic field) of the vectors cancel out and, overall, there is a resulting magnetisation vector of the entire body pointing in a direction parallel to the magnetic field.
Therefore, in the MRI machine, the body gets slightly magnetised.
Now the external magnetic field above is applied by the MRI and this field static (i.e. it remains in one direction and stays the same strength).
Magnetic field strength is measured in Tesla (T).
Most MRI machines are 3T (30,000 x Earth’s magnetic field).
Background - Resonance and RF pulses
Now that the Hydrogen nuclei are on a precession path around the magnetic field lines, they can be hit with electromagnetic waves with the resonant frequency of the precession (Larmor frequency as mentioned above). In effect, this gives the nuclei more energy. The frequency will be in the Radio spectrum of the EM wave spectrum, so it is called Radio frequency or RF. This can be generated by having a spinning transverse magnetic field, which spins with the Larmor frequency of the nuclei. Or it can be straight forward Electromagnetic waves.
There will be “pulses” of RF. This means that, if a spinning magnetic field is used, it will be turned on and allowed to spin for a certain amount of time. Or, if an electromagnetic wave is used, it will be short pulse wave.
The duration of the RF pulse will decide the amount of energy that gets “dumped” into the nuclei.
While a spinning top might smoothly increase it’s radius of precession (i.e start wobbling more and more), a subatomic particle (such as the nucleus) has quantum states, as mentioned above.
So the energy will get dumped into the spinning nucleus but it will not start wobbling more.
In fact, what will happen is: some of the nuclei will gain enough energy to flip to the higher energy anti-parallel spin.
While the others will have an increase in energy. Their precessions will become more “matched”.
This will mean that the precessions will become more “in phase” and the antiparallel spins will also become more “in phase”.
How “in phase” the precessions are depends on the energy dumped into the body, which depends on the time the RF pulse is switched on.
Depending on the amount of energy given (how long the RF pulse is turned on for), it is possible to completely remove the vertical magnetisation component, if one can match the number of parallel and anti-parallel spins, thus having a cancellation in the z (longitudinal) direction..
(This is often referred to as the 90° RF pulse as it makes the magnetisation completely in the Mxy plane and this magnetisation spins)

Diagram showing nuclear precessions after an RF pulse has been applied.
In simple terms, if we imagine just the transverse components of the spin magnetisation vector of each nuclei at a point in time before the RF pulse is applied and then at a point in time after the RF pulse is applied, the following effect will happen:

Diagram showing only the transverse magnetisation vectors of each individual nucleus, given a common axis and common centre point. The nuclei themselves have been removed from the diagram and only the transverse magnetisation vectors have been kept, purely for visual ease.
Taking all of these spins and looking at the magnetisation vector of the entire body, it can be seen that there will now be a horizontal magnetisation (perpendicular to the magnetic field) and a lower magnetisation in the vertical direction (parallel to the magnetic field).
This horizontal magnetisation vector will actually spin, as, in effect, it is a result of the precession of the nuclei.
This can now be detected as a conductive loop can be set up and the magnetic field spinning through this loop will induce a voltage (Faraday’s law of electromagnetic induction).
For the sake of simplicity, one can create a diagram where all the nuclei, in the area being imaged, are given a common axis and a common origin (i.e. the diagram imagines putting together all the nuclei in the same space).
In addition, we can freeze the nuclei at three points in time, to take snapshots of the positions of their spin magnetic moments (spin magnetisation vectors) at these times. Note: this is not exactly how it works in real life as, due to the quantum nature of sub atomic particles, it can never be ascertained if the nuclei are spin up, spin down or both (yes the nuclei can have a combination of spin up and spin down). However, as a model, this is a safe representation to aid in the understanding of this phenomenon.
Now, the nuclei, themselves, can be removed from the diagram (they are still there, but for simplicity, looking at just the spin magnetisation vectors of the nuclei makes the diagram much clearer).
With this in mind, a diagram has been presented below where:
- the light grey straight arrows show the spin magnetisation vectors of all the nuclei in the area
- the dark grey circular arrows represent the parallel and anti-parallel precession paths
- the light red squiggly arrow is the RF pulsethe dark red arrow is the resultant magnetisation vector
- the light red straight arrows are the z (Mz, or the vertical arrow) and x/y (Mxy, or the horizontal arrow) components of the resultant magnetisation vector.

Diagram showing only the magnetisation vectors of each nuclei with the nuclei removed. Contents of the diagram are explained above the diagram. Note the big grey arrows pointing right represents the progression from static field to RF excitation back to static field.
The diagram shows the RF excitation to get to the middle diagram. Then the relaxation stage follows where return to their original states (as shown in the right hand side diagram) Mz starts of being the actual magnetisation vector, then becomes smaller, then, after relaxation, goes back to being the magnetisation vector. The time taken for this relaxation period is known as longitudinal relaxation or T1. M0 represents the size of the original magnetisation vector.
T1 decay longitudinal spin-lattice relaxation
$ M_z = M_0(1-e^{\frac{-t}{T_1}}) $
As can be seen from the equation, T1 represents the time that it takes to get to 0.63 of Mz(0) (if t = T1, the equation above becomes $ M_z(t) = M_0 (1- \frac{1}{e}) $ which rearranges to Mz = 0.63M0). Remember: M0 represents the initial magnetisation vector when the magnetisation was pointed in the same direction as the magnetic field.
Mxy starts of as 0 and then becomes non-zero before going back to 0. The time taken for this relaxation period is known as transverse relaxation, T2. This occurs as the nuclei become out of phase and the spins that had flipped anti-parallel would have now returned to a parallel state and all the transverse magnetisations for each nuclei would have cancelled out between all the other nuclei again.
T2 decay transverse spin-spin relaxation
$ M_{xy}(t) = M_{xy}(0) e^{\frac{-t}{T_2}} $
From the equation, one can see that T2 represents the time taken for the Mxy to get to 37% of the initial Mxy component after the RF pulse has hit the body. Remember: Mxy(0) reopresents the transverse vector directly after exitation by the RF pulse. Therefore, it represents the maximum transverse magnetisation.

Theoretical graphs showing a comparison between T1 and T2 decay. Note that T1 decay occurs over a far longer time period as it takes much longer to recover the longitudinal magnetisations.
So the signal that is achieved from measuring the induced voltage in our conductive loop would be the following, if we measured continuously over a long period of time:

Theoretical graph showing Free Induction decay. Remember that the transverse magnetisation vector is swinging through the conductive loop. Hence, why there is this oscillatory behaviour. The equation is governed by: $ V_{xy}(t) = V_{xy}(0) e^{iw_0 t} e^{\frac{-t}{T_2}}$, where Vxy(0) is the initial voltage which was generated by the initial transverse magnetic field.
This is called Free induction Decay. The transverse magnetisation vector will spin through the current loop, getting smaller every single time. The spinning of the vector causes the oscillation and the T2 decay causes the overall exponential reduction of the induced voltage.
Key points to summarise the background:
- The nuclei all have intrinsic spin and a non-zero spin is where there are unequal number of protons and neutrons in the nucleus.
- Hence, we look at Hydrogen nuclei as they have just a proton in their nuclei
- 1H nuclei (proton) have a spin magnetic moment, which precesses along an external magnetic field (applied by the MRI machine)
- Some precess parallel; others anti-parallel and these are the only 2 states (no intermediate spin state)
- The precession has a frequency known as Larmor frequency
- An RF pulse at the Larmor frequency can be applied, causing there to be more energy in the proton
- Some protons have enough energy to flip from parallel anti-parallel, while most of these become in phase
- Creating a transverse component of magnetisation on the body
- Important: The transverse components spins and, therefore, can be detected using a conducting loop.
- The longer the RF pulse is applied, the more flipping of spins there is
- The amount of magnetisation in each direction can be controlled in this way (in effect, it is possible to get rid of the vertical component (90° RF pulse) or flip the magnetisation of the body (180° RF pulse))
Tissue contrast
Now that we understand how the magnetisation of a body can be manipulated and how a signal can be detected, let’s look at the process used to create the signal and achieve tissue contrast.
To create the signal, first of all, a 90° RF pulse is applied. Now, the spins are going through T2 decay as well as T1 decay. The transverse magnetisation vector is shortening, while the longitudinal magnetisation vector is recovering. The T1 decay takes far longer than the T2 decay.
This means that we can either focus on the T1 or the T2 components in terms of gathering a high contrast signal. If we are interested in a particular area of tissues which show high contrast in the T1 component, then the timings of signal sampling and reptition of sampling can be adjusted. Similarly for the T2 components, adjustments can be made.
After sending in the 90° RF pulse it is possible to repeat this. The time after which this repeat is done is known as TR. We can also sample the signal, which is known as echo time (TE). There are other options too, which will be discussed later.
When we send in the RF, even if the longitudinal magnetisation hasn’t fully recovered, whatever has recovered still flips to the transverse magnetisation. So, for different tissues, weaker T2 signals might be given out as will be seen in the graphs below.
The following diagram shows how to get T1 contrast and how to get T2 weighted contrast:

Theoretical graphs showing contrast levels and making a comparison between areas of high contrast in T1 decay and areas of high contrast in T2 decay. Also showing when long TE/TR and short TE/TR is used in each respective case.
For a T2 weighted image, simply, one would sample the signal at the point in time where there is the greatest difference in the size of the Mxy. This would mean a longer TR and a longer TE:

Theoretical graphs showing T1 decay and T2 decay over a similar timescale and what happens when a repeated 90 degree pulse is used and then the signals are sampled with T2 weighting in mind.
For a T1 weighted image, simply, one would sample the signal at the point in time where there is the greatest difference in the size of the Mz. This would mean a shorter TR and a shorter TE:

Theoretical graphs showing T1 decay and T2 decay over a similar timescale and what happens when a repeated 90 degree pulse is used and then the signals are sampled with T1 weighting in mind.
One thing to notice is: the Mxy changes drastically in the T2 weighted image. This is explained above as being due to the fact that the Mz has not fully recovered, hence the transverse magnetisation will be smaller.
In effect, one can imagine that the longitudinal magnetisation vector is being “flipped” 90° in order to aid the understanding behind why the start position of the T2 decay is so different for each tissue after a repeated 90° pulse.
If one looks at the T1 recovery for each tissue and then matches it up with the ones in the T2, they can see a correlation between the start points for the new T2 decay cycle and the points at which the recovery of the T1 recovery has been cut short by the 90° flip. Of course these points would not exactly be the same.
In this way, if we then immediately sample the signal, we get a very good contrast as can be seen from the pink line on the T2 decay graph, where the lines have a large distance between them. Remember that the signal is detected by the spinning transverse magnetisation, therefore, the T1 weighted image would result in an inevitable contrast, as can be seen from the graphs above.
Spin Echo
Spin Echo represents a 90° RF pulse followed by repeated 180° RF pulse. Now, as mentioned above, the amount that the vectors “flip” is governed by the duration of the RF pulse. What a 90° pulse does is:
- Pushes the precessions into coherent phase (they start spinning together at similar speeds)
- Flips spins until the number of spin ups and spin downs are almost equivalent.
Now, the 180° pulse simply flips the magnetisation vectors by a rotation of 180°:

Diagram showing the rotation of the magnetisation vectors by 180°. The rotation occurs about the rotating axis that is perpendicular to both the z axis and the resultant transverse vector.
This allows for the T2 to be recovered and for the signal strength to be stronger (remember that the transverse component is what gets detected for the signal).
Therefore, the original shorter T2 decay is known as T2$*$. The spin echo would allow for a better T2 weighted image.
The new T2 decay is a result of the continually strengthened. Now, it is important to remember that the spin echo does not affect the longitudinal magnetisation vector. So the T1 decay is not affected at all. Therefore, there will be a slower T2 decay but no changes to the T1 decay. This allows for a better tissue contrast.

Theoretical graph showing the spin echo effects on the Free induction decay in T2. As can be seen from the graph, the T2$*$ is rapid, in comparison to the T2 after the spin echo effects. Different tissues would produce different T2 decays as known from above and this will, inevitably, result in greater tissue contrast.
Note: 180° pulses are generally done at the time t = TE/2. Therefore, it is done at half the time of the sampling of the signal.
An example of a T2$*$ vs T2 weighted images is shown below. One can see much greater contrast in the brain image and lesions are much more clearly visible:

Image comparing T2$*$ (left) vs T2 (right) weighted images. Images have been gathered from the paper at http://www.ajnr.org/content/24/1/88 by authors Yoshito Tsushima, Jun Aoki and Keigo Endo.
Gradient Echo
Similar to Spin echo, but instead of a flip causing a rephasing, a gradient is applied to cause dephasing, which then will accelerate the dephasing component of the FID (opposite to spin echo effect), resulting in the transverse magnetisation going to 0 before the T2$*$ time has occured. Then a rephasing gradient is applied. This pulls the transverse magnetisation vectors back into coherent phase before they naturally decay again. This allows for faster images to be formed.

Theoretical graph showing the effects of Gradient echo on the Free Induction decay in T2
Imaging
How a signal is created and received has now been discussed in great detail. However, how one can derive an image from that has not been discussed at all. When a camera gets an image, it will take in the light via an aperture and this light will be projected onto a film or a screen or read digitally.
However, neither are there light rays being emitted from an MRI subject, nor are there apertures and screens/films to detect the “light”. It is also not like X-Rays, where the detector receives different intensities of X-Ray from the X-Rays passing through the X-Ray subject and builds up a 2D image from that.
In MRI, we only have a conductive loop to pick up the magnetic signal. While an area of the body may give different intensities based on the proton concentration in the area, it won’t dictate it’s spatial position. (The greater the density of protons in an area, the larger the transverse vector would be as it rotates through the conductive loop).
To get some spatial awareness, gradients in each direction have to be created.
Firstly, a gradient in the z-direction is created. This allows for slice by slice images to be created. Since the gradient results in there being different magnetic field strengths at each part of the patient’s body, the Larmor frequency $ \omega$ at each plane (or slice) along the z-axis would be different (remembering that $ \omega_0 = \gamma B_0 $), as the B0 would change along the body. The slice thickness would occur from taking the RF pulse in a range of frequencies. The larger the range, the thicker the slice and, hence, quicker the imaging time is.

The gradient occurs across B0, where B0 is the centre of the gradient. The slice shown, here, crosses between 2 frequencies (A and B Hz). The larger the difference between A and B, the bigger the slice. As can be seen, the frequency corresponds to the position of the body that the slice is being taken from.
So now we can choose a slice (point in the z-axis) at which to get a 2D image. But what about the x and y axes? Along the x or y axis (one of the transverse axes, say x), a gradient could be applied again. This is known as frequency encoding. This means that at all points along the x axis would have a different $\omega$ (Larmor frequency). So now we can look at it on a point by point basis, to get all the x values of the image.

Diagram showing how the gradient would be very similar in the x direction as in the z direction. Therefore, each position on the x axis corresponds with a certain frequency. A high resolution image will have a small frequency range for each point.
Now for the y or x axis (the other transverse axis, say y)? If we add another gradient magnetic field for this axis, there might be overlap of frequency at different points on the x axis. This would mean that it wouldn’t be possible to tell if it was at point A on the x axis or point B, both of which are showing the same frequency. Here, instead, we can change the phase of the precession for each point along the axis.
This will allow for no confusion in the frequency because the frequency at each point on the x axis will be unique and, therefore, all the points on the y axis at a point on the x axis will have the same frequency. But there will be an unique phase difference along all points on the y axis. Therefore, the different time points at which positions along the y axis will be in phase can be used to mark detect signals from those positions. This will allow the time points at which the signal is taken to signify the position at which the signal is taken from to find the position on the y axis.

Diagram now showing the frequency gradient in the x axis and the phase gradient in the y axis.
The resulting image is one in the frequency domain (known as k space). Then, to achieve an actual image, Fourier techniques can be used (covered in image processing).
Video
Show the physical MRI machine in more detail. Then cut to an animation and diagram.
Ultrasound
We’ve always associated images and vision with electromagnetic waves, but if we could use sound to see? This is precisely done by many animals in the animal kingdom; namely, bats are a prime example. EM waves (or in particular the visible spectrum) gives us information such as colour (within it’s frequency/wavelength) and intensity and/or amplitude. Sound waves also give us frequency and intensity and/or amplitude. However, the only information we get from sound is its pitch and loudness, which makes it difficult for us to create and visualise an image of particular interest to the human eye, from the sound alone. However, by understanding the physics of sound waves and using some clever image processing techniques, a meaningful image that can be produced.
So why use Ultrasound?
- It’s very harmless (they don’t have ionising radiation); often, radiologists say that the most harmful part of Ultrasound is a bad diagnosis!
- It is relatively much cheaper than other devices
- It is portable and have great versatility
- It is heavily applicable in soft-tissue imaging
- It is really comfortable and quick to use.
Why don’t we just use ultrasound?
- Ultrasound is often difficult to operate and understand
- The image is not as clear as MRI or CT scans
- It is very prone to false positive diagnosis, which may result in unnecessary and invasive procedures being carried out later.
- Many cancers are not detected by Ultrasound
- Not very sensitive to calcification
Sound waves and their physics
A wave is a transfer of energy through a medium in the form of oscilations within the medium. Waves can be longitudinal (the osciliations go backward and forward) or longitudinal (the waves go upwards and downwards).
The wave can be mathematically modelled as a Sinosoidal wave: $P(x,t) = P_0 sin(kx - \omega t) $. Here, $P$ represents the position, while $P_0$ represents the initial position. $\omega$ and $k$ are the frequency and wave number, respectively.
An intuitive way to make sense of this is to imagine that each particle starts of in a still position. If this is the “neutral” or rest position, then when a wave passes through, the energy of this wave is passed onto this particle (either through surrounding particles or through direct for application of a force).
This causes the particle to move (work is done on the particle). However, due to the resting position being of lowest energy, the particle wants to move back to this resting position. However, it won’t just move back and stop; it will overshoot and then feel an “attraction” back to the resting position in the other direction and then oscillate back and forth until it loses all its energy, assuming another wave hasn’t travelled through the material at this point.

Diagram showing the displacement of a particle when a pulse of energy passes through (shown here as wave energy). The pink arrow represents the attraction back to the resting position, commonly known as a restoring force.
In effect, it can be seen as being akin to a pendulum. Now, in a large material, we can model multiple of these particles together and the spread of the particles can create interesting particles. The particles can either oscillate in the direction that the wave is travelling in (longitudinal) or in the direction perpendicular to that of the wave (transverse or shear).

Diagram showing the propagation of particles in a transverse (shear) wave and in a longitudinal wave. The first pair of graphs shows when the waves enters the material and the second pair shows when the waves are fully into the material. Note the small red/pink arrows show the displacement of each of the particles.
While sound waves can have shear properties, they tend to travel with a longitudinal wave. The “ultra” part of ultrasound describes the fact that these wave frequencies are beyond that of human hearing (>20 kHz).
Piezoelectric effect
A substance that is piezoelectric tends to be able to generate a voltage when compressed and stretched.
Imagine an amount of mass with equivalent negative and positive mass. Now if this mass has its electrons (or negatively charged mass) concentrated in one part, that part is relatively more negative, in charge, and the other part is positive.
Now, if this can be compressed and stretched, the areas of negative and positive charge change and the polarity (i.e. how separated the negative and positive charges are) changes.
We know that a change in charge results in a current/voltage. Hence, the Piezoelectric effect relies on this to generate a voltage.
However, a material is only Piezoelectric if a voltage can induce such a compression and extension within the material too.
The compression and extension also results in compression of the air and extension of the material around it, which results in a wave; a sound wave.
An ultrasound transducer is made of such Piezoelectric material that has both the capability to transmit soundwaves through a given voltage and read received soundwaves through an induced voltage, generating an electrical signal.

Diagram showing the position of the charges with deformation of the mass.
Note: Once again, this is a simplistic way to look at the Piezoelectric effect and, there are much more crucial details that can be looked into but not needed to get a generic idea of the role of the Piezoelectric effect in Ultrasound.
Video
Look at the machinery in real life and go into the pictographs. Explore the piezoelectric effect.
Nuclear Imaging
Video
Microscopy
Video
Optical Coherence Tomography OCT
Video
Written by Suryava Bhattacharya & Tobias Whetton